Biological Data Science

COSC241: Lectures 22 and 23

Alex Gavryushkin

17 and 21 May 2018

Handouts

All slides are online at
You can follow this lecture at

Outline

What is data science?
What is molecular biology?
How big is big? Scalability
Online algorithms

1. Data Science (my take)

ML = Machine Learning
CoSt = Computational Statistics
AS = Applied Statistics

It's not about applying old methods to new problems

Abraham Wald

R. Siegmund-Schultze (2003). Military Work in Mathematics 1914–1945: An Attempt at an International Perspective. Mathematics and War, edited by Bernhelm Booß-Bavnbek and Jens Høyrup, 23–82. DOI: 10.1007/978-3-0348-8093-0_2

2. Molecular biology: crash course

Does this matter?

Genetics diseases, e.g. cancer
Antibiotic resistance
Virus outbreaks
Food
Ecology
Information storage?
. . .

Why is it suddenly a thing?

Why biological data science?

Because the skills are highly transferable:

Nosy data
Visualisation
Communication
High-performance computing

Formalising biology

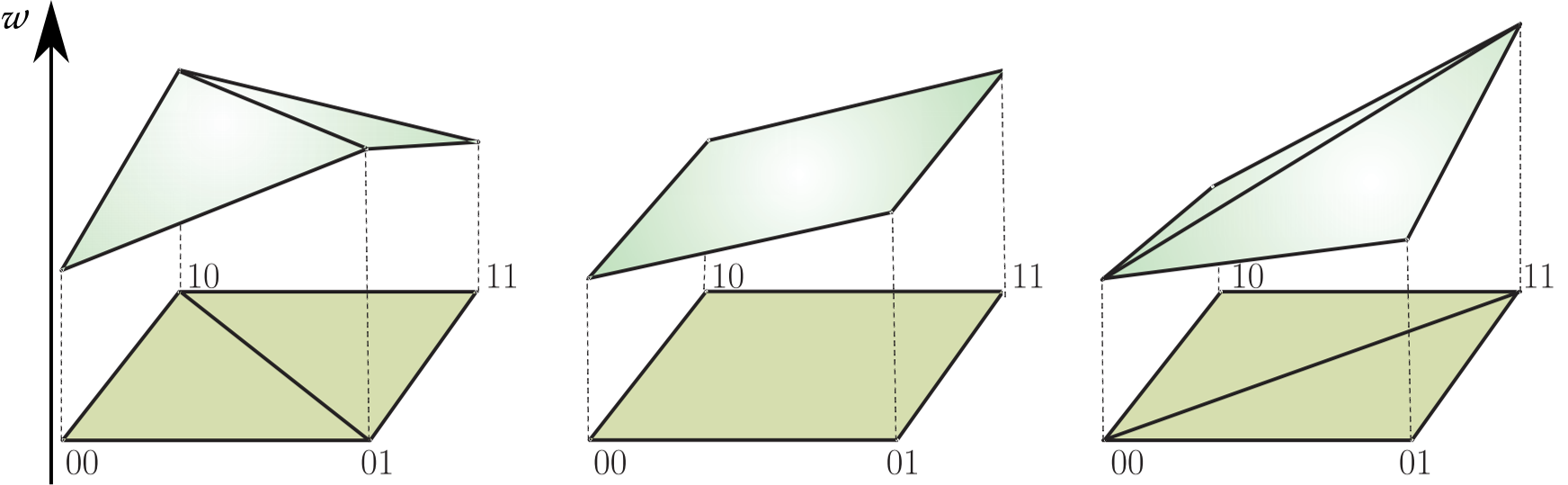
Let $G$ be the set of binary (quaternary in reality) strings of length $n$.
Elements of $G$ are called genotypes.
A function $w: G \to \mathbb R^+$ is called a fitness landscape.
For $g \in G$, $w(g)$ is called fitness of the genotype $g$.

Reality

Scalability: synthetic lethal pairs

How many pairs of genes are there in the human genome?

Gene-gene interactions

Epistasis

is defined as the deviation from the additive expectation of allelic effects: $$u_{11} = w_{00} + w_{11} - (w_{01} + w_{10})$$

Understanding three-way interactions

Marginal epistasis?

$\small u_{\color{blue}{0}11} = w_{\color{blue}{0}00} + w_{\color{blue}{1}00} + w_{\color{blue}{0}11} + w_{\color{blue}{1}11} − (w_{\color{blue}{0}01} + w_{\color{blue}{1}01}) − (w_{\color{blue}{0}10} + w_{\color{blue}{1}10})$

Total three-way interaction?

$\small u_{111} = w_{000} + w_{011} + w_{101} + w_{110} - (w_{001} + w_{010} + w_{100} + w_{111})$

Conditional epistasis?

$\small e = w_{\color{blue}{0}00} − w_{\color{blue}{0}01} − w_{\color{blue}{0}10} + w_{\color{blue}{0}11}$

What if no (credible) fitness measurements are available?

Image: Wikipedia

Mutation fitness graph

Ogbunugafor et al. Malar. J. 2016

Rank orders. The simplest case.

$\small u_{11} = w_{00} + w_{11} - (w_{01} + w_{10})$

Exercise: Dyck word algorithm

$$ \begin{align} \small u_{011} =~ & w_{000} + w_{100} + w_{011} + w_{111} − \\ & w_{001} - w_{101} − w_{010} - w_{110} \end{align} $$

$$ w_{111} > w_{011} > w_{101} > w_{010} > w_{000} > w_{110} > w_{100} > w_{001} $$

$$ w_{111} > w_{011} > w_{100} > w_{000} > w_{001} > w_{101} > w_{010} > w_{110} $$

A way to quantify uncertainties!

Crona, Gavryushkin, Greene, and Beerenwinkel. Inferring genetic interactions from comparative fitness data. eLife, 2017.

Connection between rank orders and mutation graphs

$\small u_{11} = w_{00} + w_{11} - (w_{01} + w_{10})$

Theorem. A partial order (e.g. fitness graph) implies epistasis if and only if all linear extensions compatible with the partial order do.

Mutation graph

Lienkaemper, Lamberti, Drain, Beerenwinkel, and Gavryushkin. The geometry of partial fitness orders and an efficient method for detecting genetic interactions. Journal of Mathematical Biology, 2018.