The geometry and combinatorics of phylogenetic tree spaces


Alex Gavryushkin


16 October 2018

What this talk is NOT about


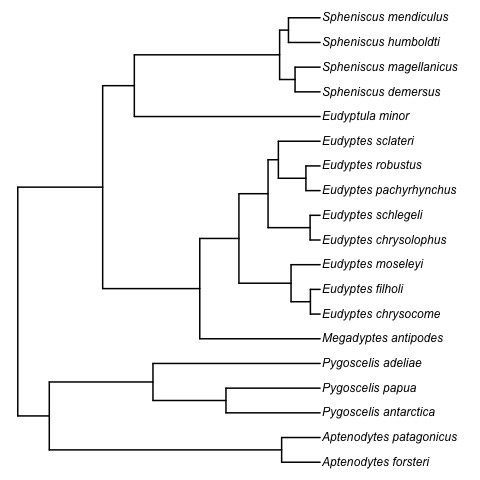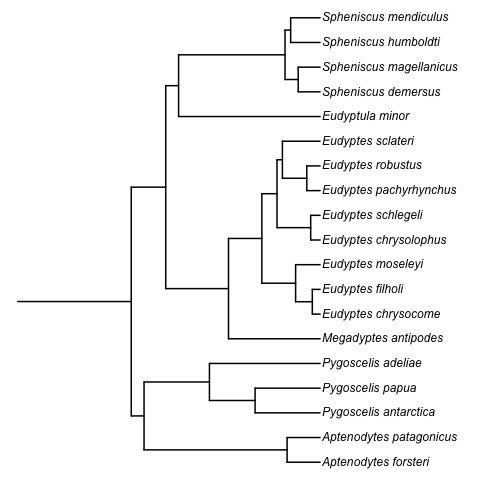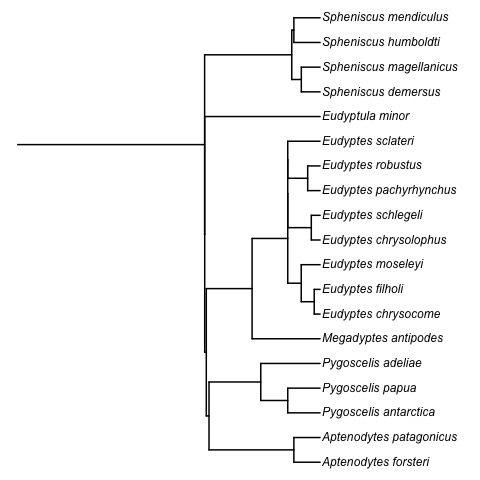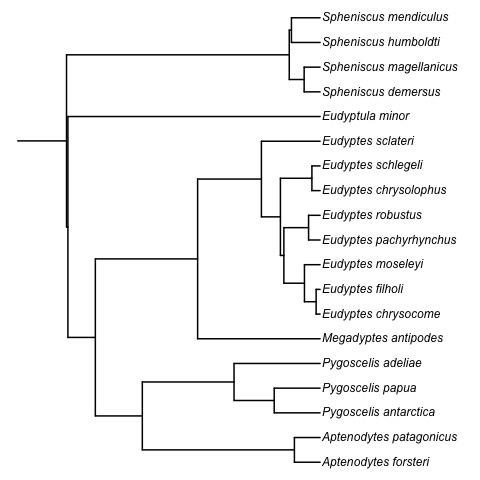
Phylogenetic inference


Image source: Wikipedia

Tumour evolution

Jahn, Katharina, Jack Kuipers, and Niko Beerenwinkel. "Tree inference for single-cell data." Genome biology 17.1 (2016): 86.

Timing tumour evolution

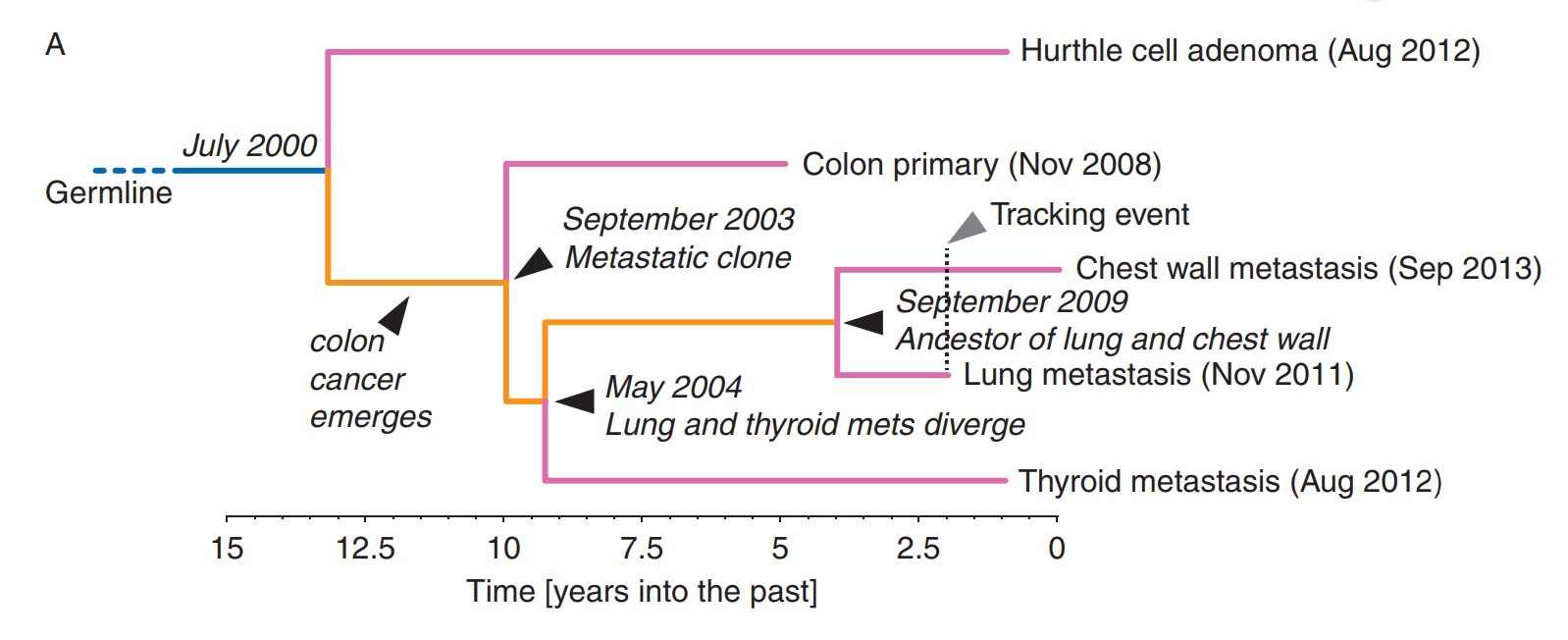
Lote, H., I. Spiteri, L. Ermini, A. Vatsiou, A. Roy, A. McDonald, N. Maka, et al. 2017. "Carbon Dating Cancer: Defining the Chronology of Metastatic Progression in Colorectal Cancer." Annals of Oncology 28 (6): 1243–49.

  • Gavryushkin, Alex, and Alexei J. Drummond. "The space of ultrametric phylogenetic trees." Journal of Theoretical Biology 403 (2016): 197-208.
  • Stadler, Tanja, Timothy G. Vaughan, Alex Gavryushkin, Stephane Guindon, Denise Kühnert, Gabriel E. Leventhal, Alexei J. Drummond. "How well can the exponential-growth coalescent approximate constant-rate birth-death population dynamics?" Proc. R. Soc. B. Vol. 282. No. 1806. The Royal Society, 2015.

tau-space

Geodesic in time-tree space

  • Gavryushkin, Alex, and Alexei J. Drummond. "The space of ultrametric phylogenetic trees." Journal of Theoretical Biology 403 (2016): 197-208.
  • Gavryushkin, Alex, and Alexei Drummond. tauGeodesic. Mar. 2015. doi: 10.5281/zenodo.47152. https://github.com/gavruskin/tauGeodesic
  • Gavryushkina, Alexandra, Tracy A. Heath, Daniel T. Ksepka, Tanja Stadler, David Welch, and Alexei J. Drummond. "Bayesian total-evidence dating reveals the recent crown radiation of penguins." Systematic Biology 66.1 (2016): 57-73.
  • Gavryushkin, Alex, and Alexei Drummond. tauGeodesic. Mar. 2015. doi: 10.5281/zenodo.47152. https://github.com/gavruskin/tauGeodesic

t-space: simplex

t-space: 2D

t-space: 3D

(Discrete) Timer-tree

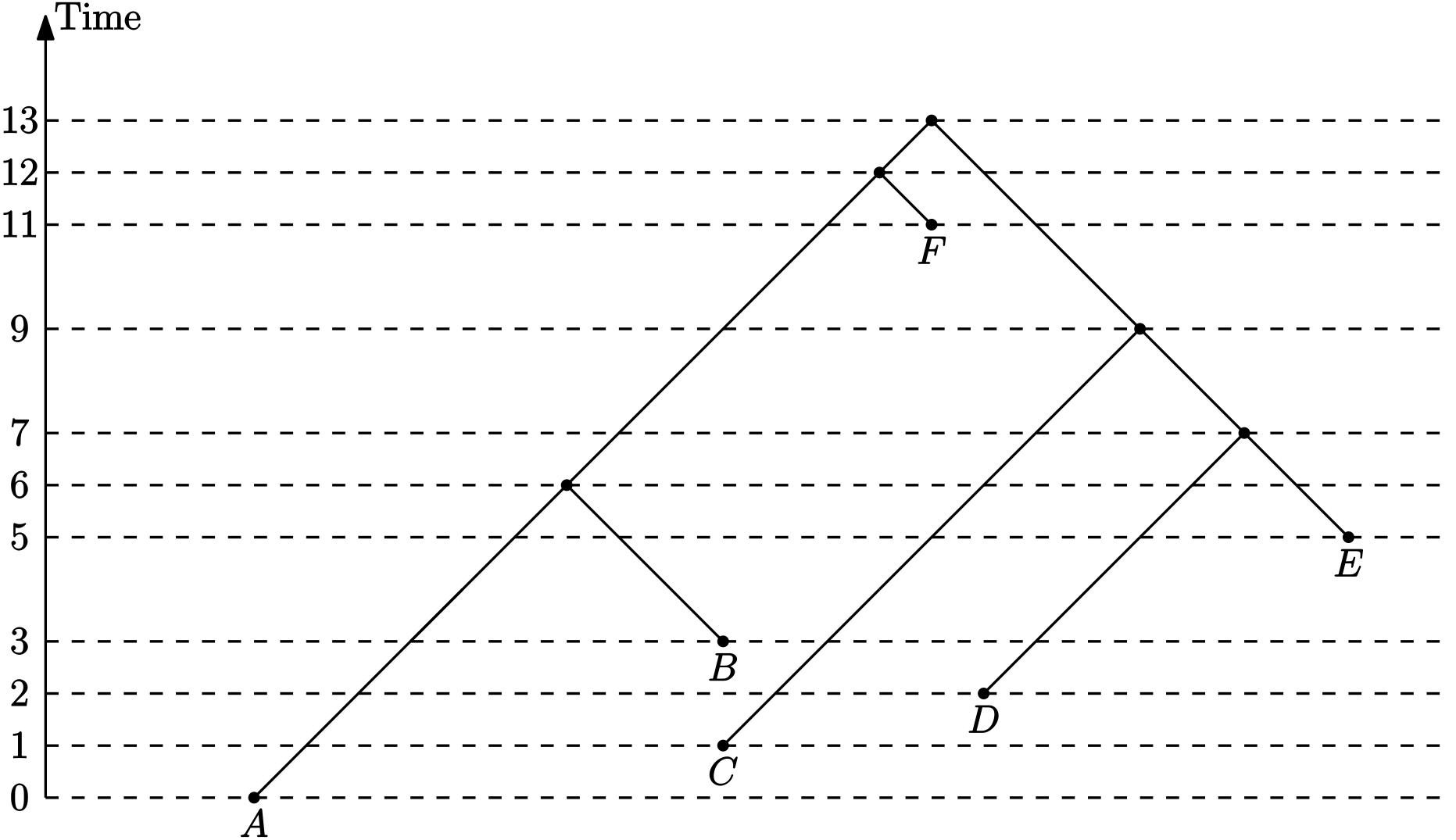
Sampled ancestor tree

NNI graph

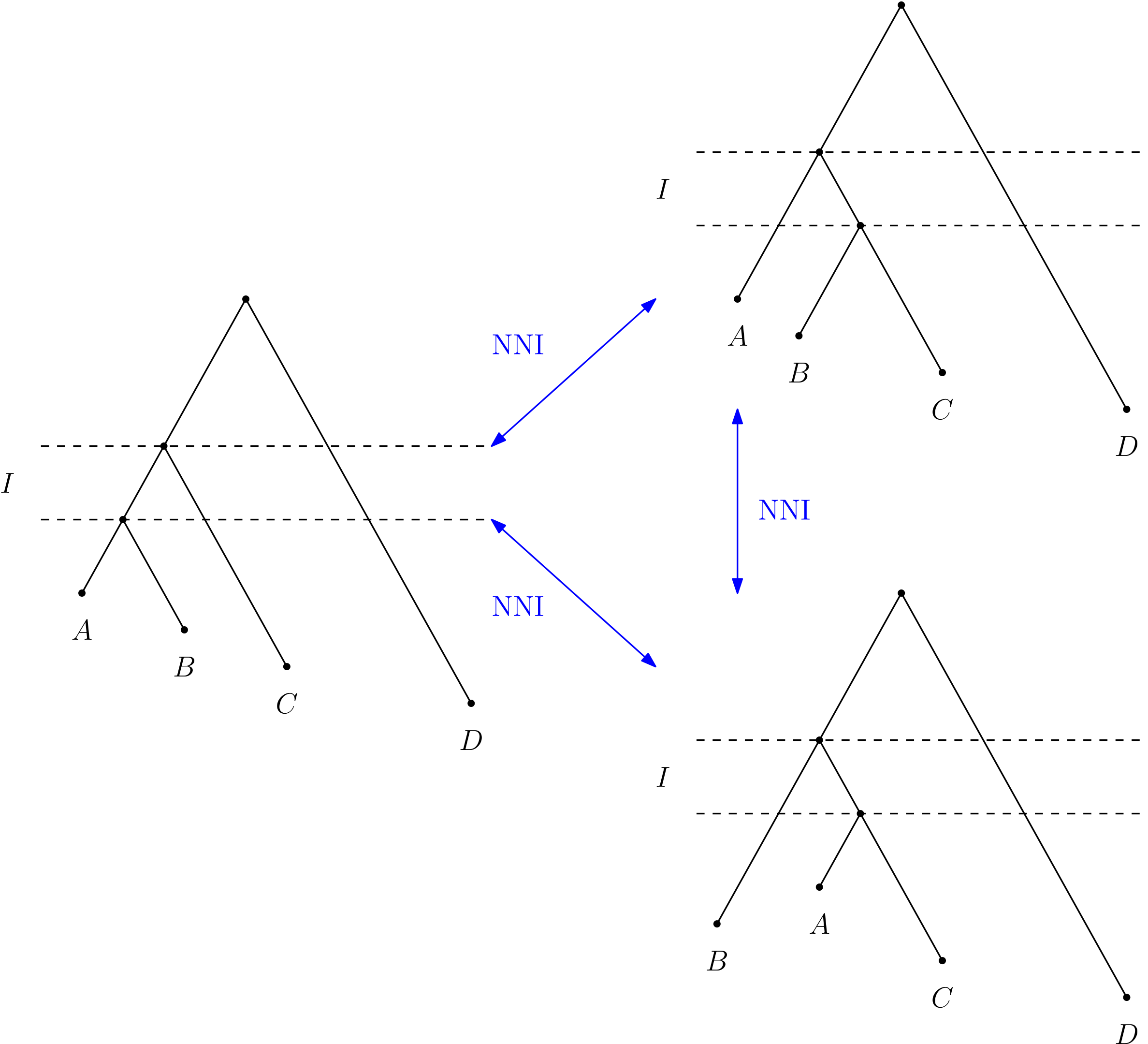
Why is this important?

  • Tree search algorithms
  • Model testing/selection and other simulation studies

Why is this hard?

Trees are many!

Discrete time-tree space

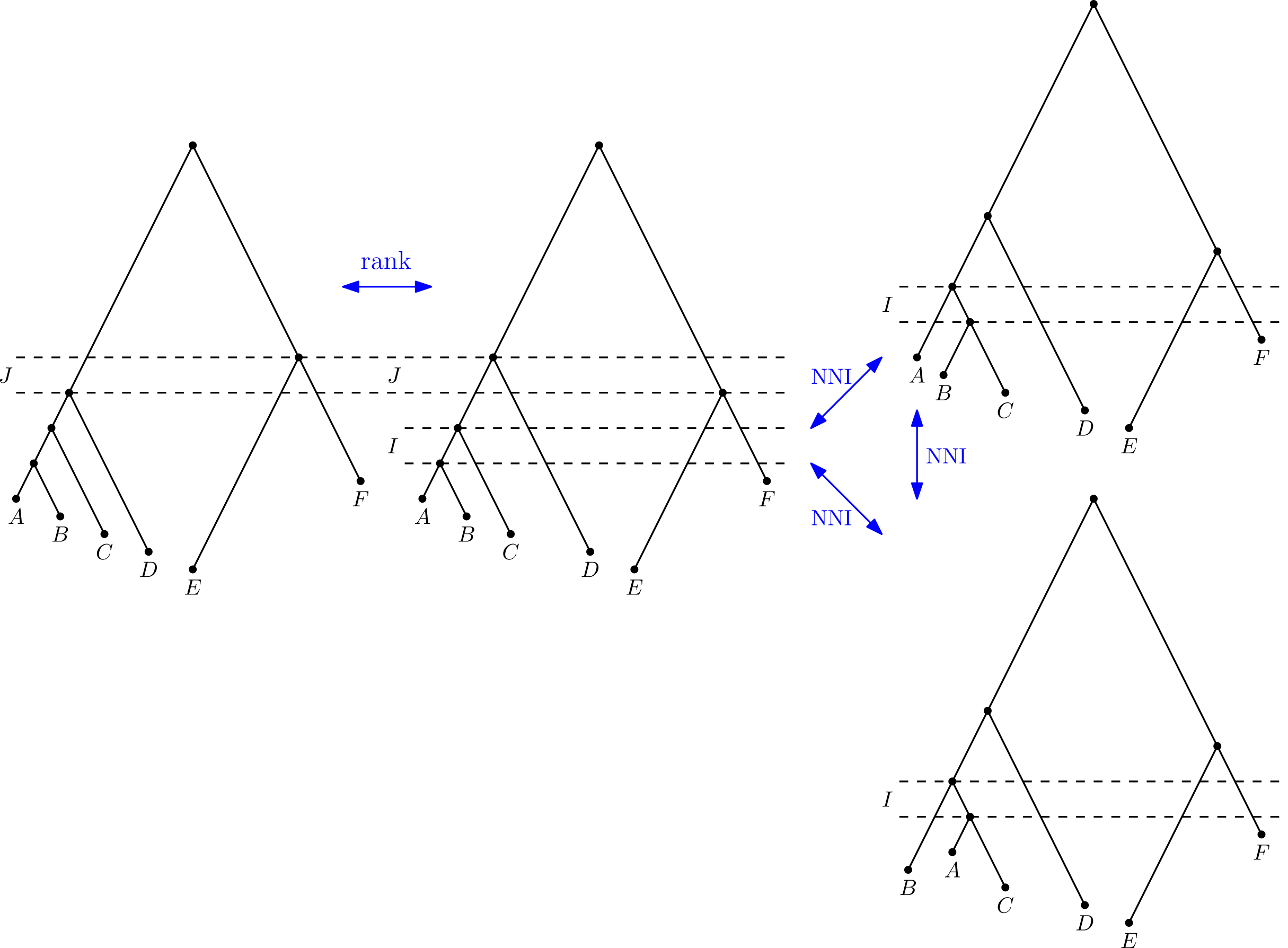
Sampled ancestor tree space

Trees at distance 2

Trees at distance 4

Main idea

(my failed proof)

History of the NNI graph

  • Over 25 year of work!
  • Over 7 erroneous papers published!

What's wrong with the NNI graph?

  1. The Split Theorem

  2. The merge and sort trick

Merge and sort trick

Merge and sort trick

RNNI is free from all these!

  • Split theorem. Tick.
  • Merge and sort doesn't work. Tick

  • Efficient polynomial algorithm?

What is an approximate (?) algorithm?

Graph grammars

A graph grammar consists of a finite set of productions $\{L_i \to_i R_i\}$, where $L_i$ and $R_i$ are connected undirected edge-end labeled graphs and $\to_i$ is a one-to-one map between half-edges of $L_i$ and those of $R_i$.

The productions are then applied to the starting tree $T$ to derive all possible trees at $\mathrm{RNNI}$ distance up to $r$ from $T$.

A production is said to be ready at a stage $s$ of the derivation if the running tree at stage $s$ has a subgraph isomorphic to the left side $L_i$ of the production.

Graph grammar: example

Theorem (Sleator, Tarjan, and Thurston). Let $\mathcal{G}$ be a graph grammar and $G$ a graph on $n$ vertices. Then the number of trees at distance at most $r$ from $G$ is $(c+1)^{n+rm}$, where $c$ is the number of vertices in left sides of $\mathcal{G}$ and $m$ the maximum number of vertices in any right side of $\mathcal{G}$.
Theorem (Sleator, Tarjan, and Thurston). Let $\mathcal{G}$ be a graph grammar and $G$ a graph on $n$ vertices. Then the number of trees at distance $r$ from $G$ is $(c+1)^{n+rm}$.

Theorem (Gavryushkin, Whidden, and Matsen). The number of trees within distance $r$ from any given tree is at most
$3^{n+2r−1}$ in $\mathrm{RNNIu}$         $3^{2n+2r−1}$ in $\mathrm{RNNI}$
$4^{n+2r−1}$ in $\mathrm{DtT}$             $4^{2n+2r−1}$ in $\mathrm{DtTu}$

Corollary (Gavryushkin, Whidden, and Matsen). $$\frac{1}{2} \log_3 \frac{(n-1)!n!}{6^{n-1}} \leq \mathrm{Diam}(\mathrm{RNNIu}) \leq n^2 - 3n - \frac{5}{8}$$

Proof:

What we've done?

  • Introduced the RNNI graph on ranked trees (to the best of our knowledge)

  • Established basic geometric properties of the graph

  • Designed an efficient approximate algorithm for computing shortest paths

  • Proved that all the fancy NNI methods, e.g. Sleator-Tarjan-Thurston and merge-and-sort argument, don't work

  • Failed to prove that RNNI is NP-hard

What has to be done?

  • Is RNNI polynomial? Complexity?
  • Split Theorem
  • Are these two related?
  • ...