Fitness landscapes, genetic interactions, and inexact data


Alex Gavryushkin


24 April 2018

We consider biallelic "genotypes" of length $n$


Example: $n = 6$

Throughout, we consider $n$ biallelic loci, for different $n$.

That is, the set of genotypes is $\mathcal G = \{0,1\}^{n}$.

A fitness landscape is a function $w:\mathcal G \to \mathbb R^+$.

For $g \in \mathcal G$,  $w(g)$ is called the fitness of genotype $g$ and denoted $w_g$.

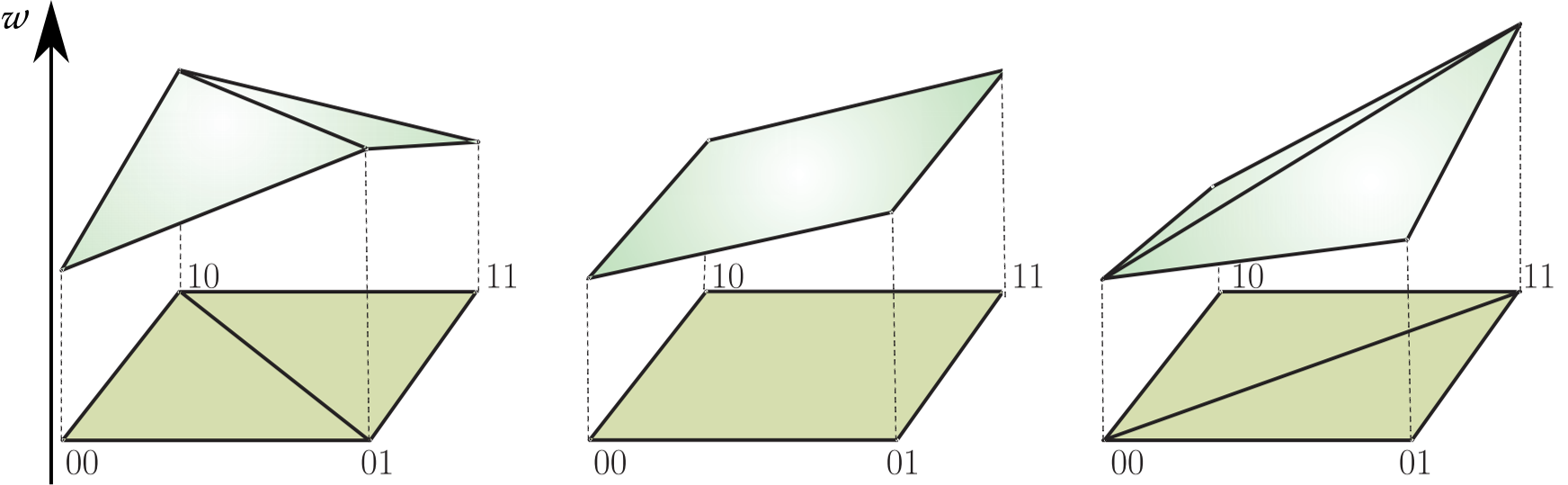
Epistasis

is defined as the deviation from the additive expectation of allelic effects: $$u_{11} = w_{00} + w_{11} - (w_{01} + w_{10})$$

Understanding three-way interactions

Marginal epistasis?

$\small u_{\color{blue}{0}11} = w_{\color{blue}{0}00} + w_{\color{blue}{1}00} + w_{\color{blue}{0}11} + w_{\color{blue}{1}11} − (w_{\color{blue}{0}01} + w_{\color{blue}{1}01}) − (w_{\color{blue}{0}10} + w_{\color{blue}{1}10})$

Total three-way interaction?

$\small u_{111} = w_{000} + w_{011} + w_{101} + w_{110} - (w_{001} + w_{010} + w_{100} + w_{111})$

Conditional epistasis?

$\small e = w_{\color{blue}{0}00} − w_{\color{blue}{0}01} − w_{\color{blue}{0}10} + w_{\color{blue}{0}11}$

Interaction classification

$e = \displaystyle\frac{u_{011} + u_{111}}{2}$

In general, the four interaction coordinates $$ u_{011}, u_{101}, u_{110}, u_{111} $$ allow to describe all possible kinds of interaction!

There are 20 types of "minimal" interactions and they are known as circuits

Yep, we've got the list!

$$ \scriptsize \begin{align*} a&= w_{000}-w_{010}-w_{100}+w_{110} & m&=w_{001}+w_{010}+w_{100}-w_{111}-2w_{000}\\ b&=w_{001}-w_{011}-w_{101}+w_{111} & n&=w_{011}+w_{101}+w_{110}-w_{000}-2w_{111}\\ c&=w_{000}-w_{001}-w_{100}+w_{101} & o&=w_{010}+w_{100}+w_{111}-w_{001}-2w_{110}\\ d&=w_{010}-w_{011}-w_{110}+w_{111} & p&=w_{000}+w_{011}+w_{101}-w_{110}-2w_{001}\\ e&=w_{000}-w_{001}-w_{010}+w_{011} & q&=w_{001}+w_{100}+ w_{111}-w_{010}-2w_{101}\\ f&=w_{100}-w_{101}-w_{110}+w_{111} & r&=w_{000}+w_{011}+ w_{110}-w_{101}-2w_{010}\\ g&=w_{000}-w_{011}-w_{100}+w_{111} & s&=w_{000}+w_{101}+ w_{110}-w_{011}-2w_{100}\\ h&=w_{001}-w_{010}-w_{101}+w_{110} & t&=w_{001}+w_{010}+w_{111}-w_{100}-2w_{011}\\ i&=w_{000}-w_{010}-w_{101}+w_{111}\\ j&=w_{001}-w_{011}-w_{100}+w_{110}\\ k&=w_{000}-w_{001}-w_{110}+w_{111}\\ l&=w_{010}-w_{011}-w_{100}+w_{101}\\ \end{align*} $$
$$ \scriptsize \begin{align*} a&= w_{000}-w_{010}-w_{100}+w_{110} & m&=w_{001}+w_{010}+w_{100}-w_{111}-2w_{000}\\ b&=w_{001}-w_{011}-w_{101}+w_{111} & n&=w_{011}+w_{101}+w_{110}-w_{000}-2w_{111}\\ c&=w_{000}-w_{001}-w_{100}+w_{101} & o&=w_{010}+w_{100}+w_{111}-w_{001}-2w_{110}\\ d&=w_{010}-w_{011}-w_{110}+w_{111} & p&=w_{000}+w_{011}+w_{101}-w_{110}-2w_{001}\\ e&=w_{000}-w_{001}-w_{010}+w_{011} & q&=w_{001}+w_{100}+ w_{111}-w_{010}-2w_{101}\\ f&=w_{100}-w_{101}-w_{110}+w_{111} & r&=w_{000}+w_{011}+ w_{110}-w_{101}-2w_{010}\\ \color{blue}{g}&\hskip{2pt}\color{blue}{=w_{000}-w_{011}-w_{100}+w_{111}} & s&=w_{000}+w_{101}+ w_{110}-w_{011}-2w_{100}\\ h&=w_{001}-w_{010}-w_{101}+w_{110} & t&=w_{001}+w_{010}+w_{111}-w_{100}-2w_{011}\\ i&=w_{000}-w_{010}-w_{101}+w_{111}\\ j&=w_{001}-w_{011}-w_{100}+w_{110}\\ k&=w_{000}-w_{001}-w_{110}+w_{111}\\ l&=w_{010}-w_{011}-w_{100}+w_{101}\\ \end{align*} $$

This is known as Beerenwinkel-Pachter-Sturmfels approach,

which provides a complete picture of interactions!

BUT

the approach is

  • based on the availability of fitness measurements

  • computationally feasible for up to four loci

Hence, we come to two research questions

Problem 1: What if no (credible) fitness measurements are available?

Image: Wikipedia

Mutation fitness graph


Ogbunugafor et al. Malar. J. 2016

Rank orders. The simplest case.

$\small u_{11} = w_{00} + w_{11} - (w_{01} + w_{10})$

Exercise: Dyck word algorithm

$$ \begin{align} \small u_{011} =~ & w_{000} + w_{100} + w_{011} + w_{111} − \\ & w_{001} - w_{101} − w_{010} - w_{110} \end{align} $$

$$ w_{111} > w_{011} > w_{101} > w_{010} > w_{000} > w_{110} > w_{100} > w_{001} $$

$$ w_{111} > w_{011} > w_{100} > w_{000} > w_{001} > w_{101} > w_{010} > w_{110} $$

A way to quantify uncertainties!

Interactions in HIV-1

Mutation graph

Connection between rank orders and mutation graphs

Applications

  • HIV-1

  • Antibiotic resistance

  • Gut microbiome (with Will Ludington, UC Berkeley)

  • Synthetic lethality

  • Knockdown cell lines

Methodologically, this allows us to advise further measurements (experiments) for incomplete data sets, thus reducing the number of potential experiments significantly.

Example: antibiotic resistance

Mira et al. PLOS ONE, 2015

Example: antibiotic resistance

Example: antibiotic resistance

Example: antibiotic resistance

Mutation graph

Mutation graph

Mutation graph

Mutation graph

Mutation graph

Results in more detail

Efficient methods for:
  • Circuit interaction inference (including epistasis and three-way interaction) for total orders
  • Complete analysis of partial orders (including mutation graphs) with "distance to interaction" inference
  • Suggestions for possible completions in case of missing data and/or high uncertainty


Software (pre-release stage):
https://github.com/gavruskin/fitlands

Problem 2: What if the number of genes (loci) is 20,822?

  • 2^20822 of conditional epistases?
  • 2^20822 measurements to estimate marginal epistasis?

Not in this life

Concrete example: genome-wide RNAi perturbation screens

20,822 genes, 90,000 "trials" (siRNA's)

RNAi perturbation screen

Two ways out

  1. Isolate a small number of "interesting" genes, e.g. main fitness drivers (like we did in the HIV study)
  2. Add statistical assumptions, for example:

    • Ignore higher-order interactions

    • Structural hypotheses: "It rarely make sense to have interactions without main effects"—Lim and Hastie


(Ongoing work with Schmich, Szczurek, Beerenwinkel, et al.)

Want to learn more?

We've got you covered!

Acknowledgements

  • You
  • Niko Beerenwinkel, ETH Zürich
  • Bernd Sturmfels, Max Planck Institute Leipzig
  • Kristina Crona, American University
  • Devin Greene, American University
  • Lisa Lamberti, ETH Zürich
  • Caitlin Lienkaemper, Penn State

and stay tuned