Polyhedral complexes in phylogenetics
and gene interaction studies

Alex Gavryushkin

August 1, 2017

Phylogenetics

Input:

  • Evolutionary model
  • Data (amino acid sequences, sampling times, geographic information, transmission information, etc.)


Output:

Time trees

Two possible parameterizations:
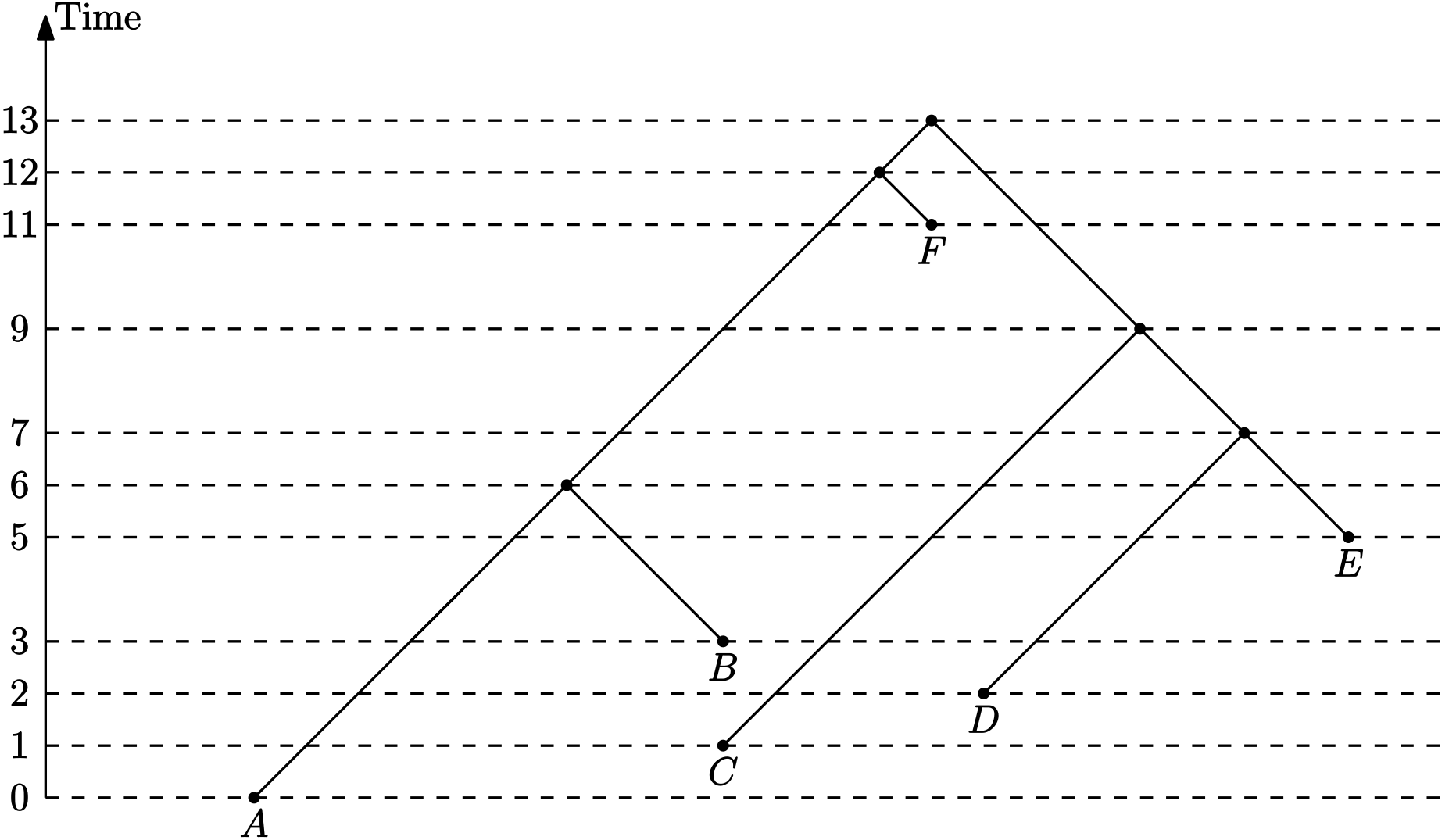
  • Absolute (calendar) time, as above
  • Distance between evolutionary events

Distance between evolutionary events ($\tau$-space)


Gavryushkin, Alex, and Alexei J. Drummond. "The space of ultrametric phylogenetic trees." Journal of theoretical biology 403 (2016): 197-208.
Theorem 1. $\tau$-space is non-positively curved cubical complex, that is, piecewise Euclidean geodesics are unique.

Theorem 2. Geodesics in $\tau$-space are computable in $\mathcal O(n^4)$ time, where $n$ is the number of leaves.
Implementation: https://github.com/gavruskin/tauGeodesic
Gavryushkin, Alex, and Alexei J. Drummond. "The space of ultrametric phylogenetic trees." Journal of theoretical biology 403 (2016): 197-208.
  • Gavryushkin, Alex, and Alexei J. Drummond. "The space of ultrametric phylogenetic trees."
  • Gavryushkin, Alex, and Alexei Drummond. tauGeodesic. Mar. 2015. doi: 10.5281/zenodo.47152.
  • Gavryushkina, Alexandra, Tracy A. Heath, Daniel T. Ksepka, Tanja Stadler, David Welch, and Alexei J. Drummond. "Bayesian total-evidence dating reveals the recent crown radiation of penguins." Systematic Biology 66.1 (2016): 57-73. https://github.com/gavruskin/tauGeodesic

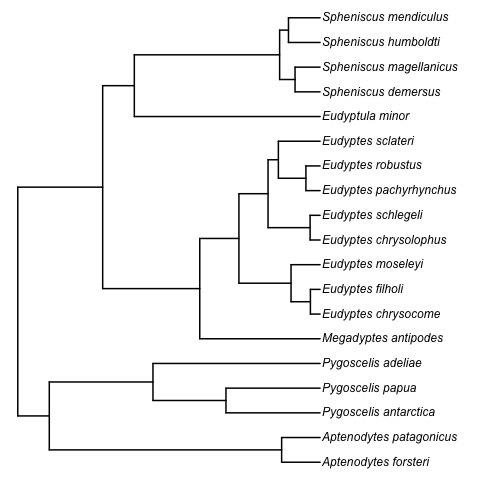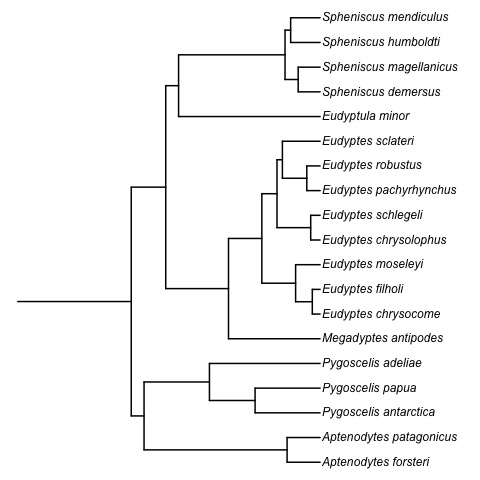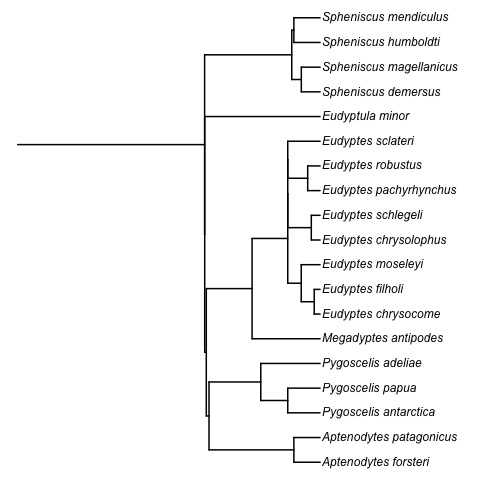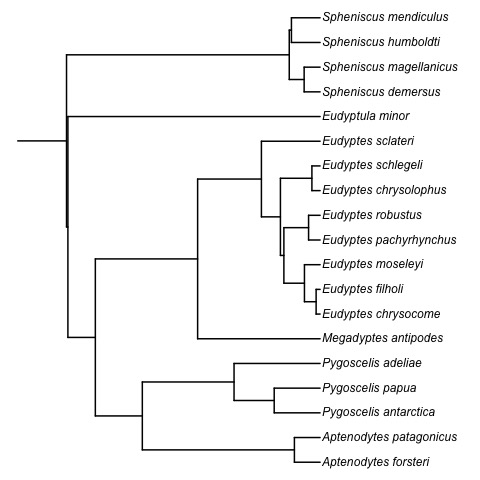
Absolute time of evolutionary events (t-space)

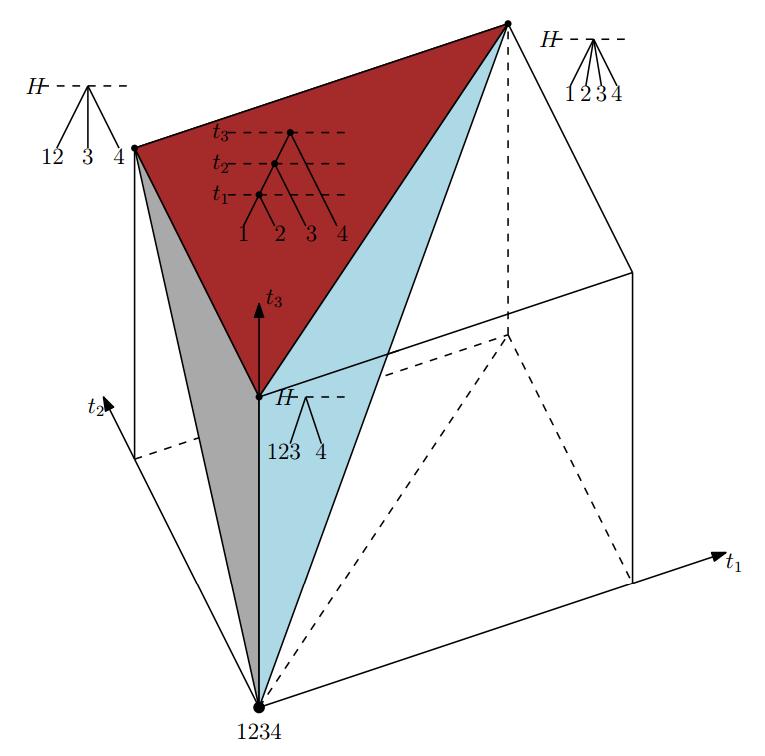
Absolute time of evolutionary events (t-space)

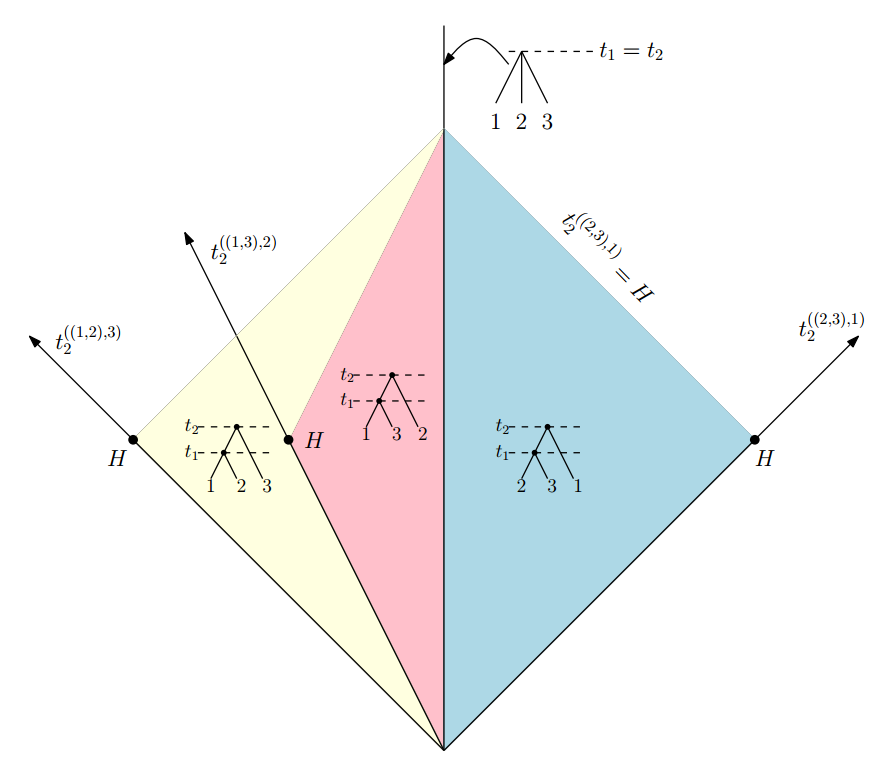
Absolute time of evolutionary events (t-space)

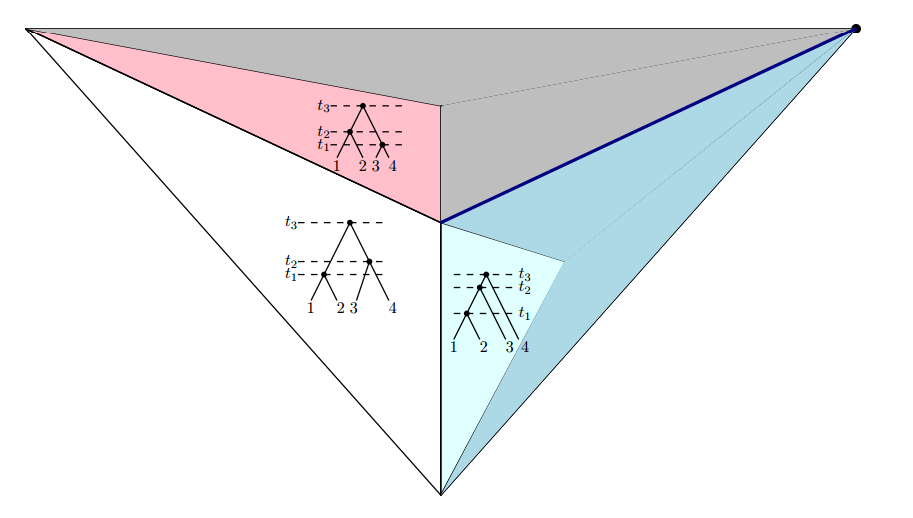
Theorem 3. t-space is a non-positively curved simplicial complex.

Question 1. What is the complexity of computing geodesics in t-space?
Gavryushkin, Alex, and Alexei J. Drummond. "The space of ultrametric phylogenetic trees." Journal of theoretical biology 403 (2016): 197-208.
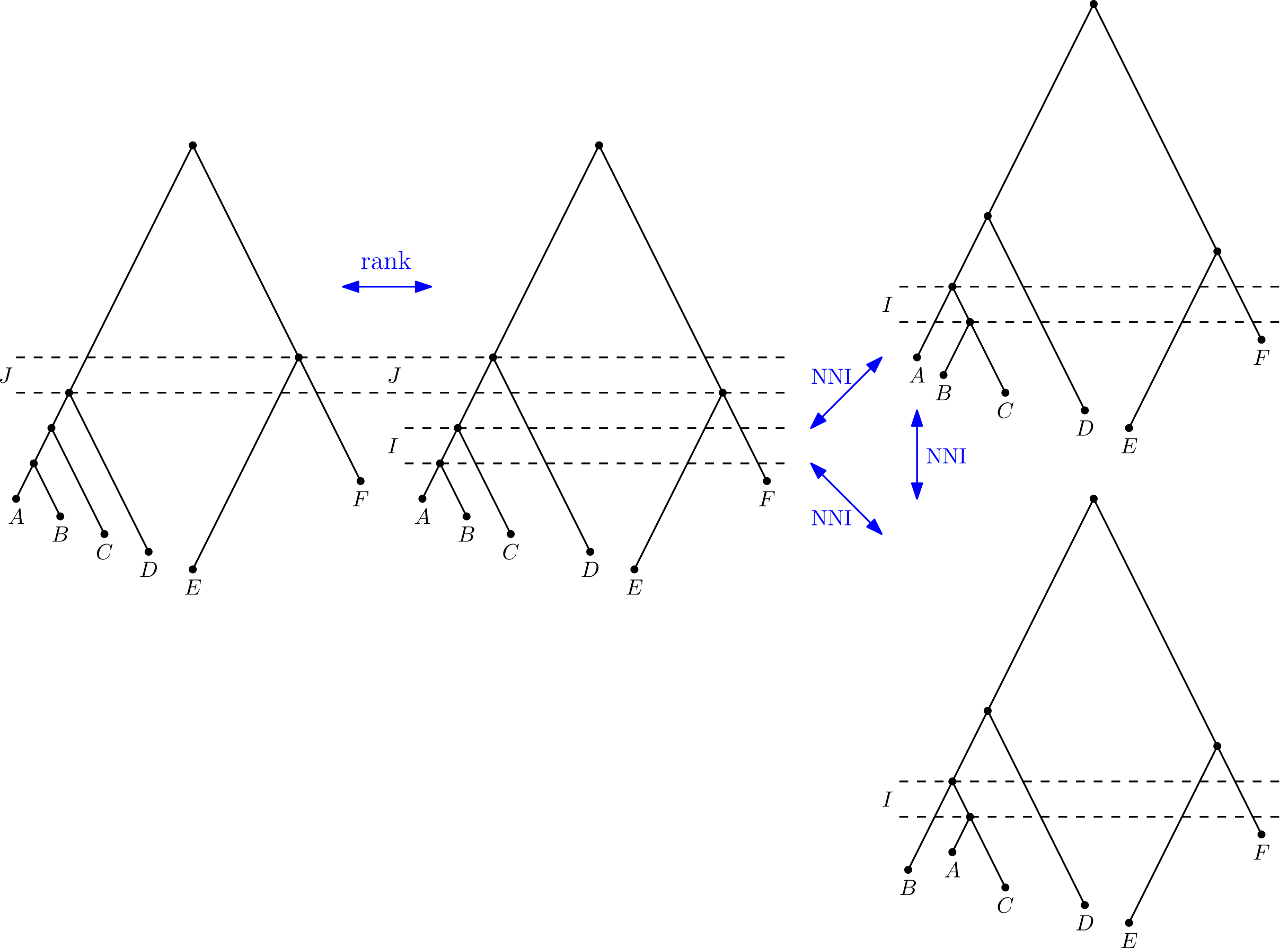
Observation. The discrete component of t-space is a new graph on phylogenetic trees, geometrically and algorithmically different from all those previously known in phylogenetics, including NNI, SPR, and TBR.

Gavryushkin, Alex, Chris Whidden, and Frederick Matsen. "The combinatorics of discrete time-trees: theory and open problems." Journal of Mathematical Biology, (2017), DOI 10.1007/s00285-017-1167-9

Note. All previously known graph-distances, including NNI, SPR, and TBR, on phylogenetic trees are NP-hard to compute.

Question 2. Is the ranked NNI graph-distance (as above) polynomial-time computable?


Gavryushkin, Alex, Chris Whidden, and Frederick Matsen. "The combinatorics of discrete time-trees: theory and open problems." Journal of Mathematical Biology, (2017), DOI 10.1007/s00285-017-1167-9

Genetic interactions

  • All commonly used models of sequence evolution assume independence between sites.
  • However, there is biological evidence that in many cases sites are not independent.
  • Furthermore, this non-independence is used more and more widely, e.g. in drug discovery and design using synthetic lethal gene pairs.
We consider $n$ biallelic loci, for different $n$.

That is, the set of genotypes is $\mathcal G = \{0,1\}^{n}$.

A fitness landscape is a function $w:\mathcal G \to \mathbb R^+$.

For $g \in \mathcal G$,  $w(g)$ is called the fitness of genotype $g$ and denoted $w_g$.

Epistasis, or gene interaction,

is defined as the deviation from the additive expectation of allelic effects: $$u_{11} = w_{00} + w_{11} - (w_{01} + w_{10})$$

Higher order interactions: interaction coordinates


$$ \scriptsize \begin{align*} u_{011}&= w_{000}+w_{100}+w_{011}+w_{111}−(w_{001}+w_{101})−(w_{010}+w_{110})\\ u_{101}&= w_{000}+w_{010}+w_{101}+w_{111}−(w_{001}+w_{011})−(w_{100}+w_{110})\\ u_{110}&= w_{000}+w_{001}+w_{110}+w_{111}−(w_{010}+w_{011})−(w_{100}+w_{101})\\ u_{111}&= w_{000}+w_{011}+w_{101}+w_{110}−(w_{001}+w_{010}+w_{100}+w_{111})\\ \end{align*} $$

Beerenwinkel, Niko, Lior Pachter, and Bernd Sturmfels. "Epistasis and shapes of fitness landscapes." Statistica Sinica (2007): 1317-1342.

Higher order interactions: circuits

$$ \scriptsize \begin{align*} a&= w_{000}-w_{010}-w_{100}+w_{110} & m&=w_{001}+w_{010}+w_{100}-w_{111}-2w_{000}\\ b&=w_{001}-w_{011}-w_{101}+w_{111} & n&=w_{011}+w_{101}+w_{110}-w_{000}-2w_{111}\\ c&=w_{000}-w_{001}-w_{100}+w_{101} & o&=w_{010}+w_{100}+w_{111}-w_{001}-2w_{110}\\ d&=w_{010}-w_{011}-w_{110}+w_{111} & p&=w_{000}+w_{011}+w_{101}-w_{110}-2w_{001}\\ e&=w_{000}-w_{001}-w_{010}+w_{011} & q&=w_{001}+w_{100}+ w_{111}-w_{010}-2w_{101}\\ f&=w_{100}-w_{101}-w_{110}+w_{111} & r&=w_{000}+w_{011}+ w_{110}-w_{101}-2w_{010}\\ g&=w_{000}-w_{011}-w_{100}+w_{111} & s&=w_{000}+w_{101}+ w_{110}-w_{011}-2w_{100}\\ h&=w_{001}-w_{010}-w_{101}+w_{110} & t&=w_{001}+w_{010}+w_{111}-w_{100}-2w_{011}\\ i&=w_{000}-w_{010}-w_{101}+w_{111}\\ j&=w_{001}-w_{011}-w_{100}+w_{110}\\ k&=w_{000}-w_{001}-w_{110}+w_{111}\\ l&=w_{010}-w_{011}-w_{100}+w_{101}\\ \end{align*} $$

Beerenwinkel, Niko, Lior Pachter, and Bernd Sturmfels. "Epistasis and shapes of fitness landscapes." Statistica Sinica (2007): 1317-1342.

Problem: What if no (credible) fitness measurements are available?

Like in this malaria drug resistance data set:
Ogbunugafor et al. Malar. J. 2016

Why is fitness hard to measure?

Wikipedia

When partial order implies interaction?


We say that a partial order $\prec$ on the set of genotypes $\mathcal G = \{g_1,\ldots, g_m\}$ implies positive $f$-interaction if \[ f(w_{g_1},\ldots, w_{g_m}) > 0 \] whenever the genotypes $\mathcal G$ are ordered according to $\prec$.
Theorem 1. Let $f$ be a linear form with integer coefficients. Assume that the sum of the coefficients of $f$ is zero. Then a linear order $L$ implies $f$-interaction iff the signs of coefficients of $f$ ordered according to $L$ form a Dyck word.

Theorem 2. A partial order implies $f$-interaction exactly if all its total extensions do.

Let $N$ be the set of genotypes with negative coefficients in $f$ and $P$ with positive. We can think of a partial order $\prec$ as of a directed bipartite graph $G$ on $N \cup P$.

Conjecture 3. Theorem 3. A partial order $\prec$ implies interaction iff the graph $G$ has a perfect matching.

Crona, Gavryushkin, Greene, and Beerenwinkel. Inferring genetic interactions from comparative fitness data. bioRxiv. eLife, under revision.
Lienkaemper, Drain, Lamberti, and Gavryushkin. Inferring genetic interactions from partial fitness orders. bioRxiv, to appear this month.

Major challenges



What do we do when $n$ is large?

  • Triangulations of the convex hull?
  • What are the canonical interactions?
  • How to interpret the result?

Applications

  • HIV-1

  • Antibiotic resistance

  • Gut microbiome (with Will Ludington, UC Berkeley)

  • Synthetic lethality

  • Knockdown cell lines

Methodologically, this allows us to advise further measurements (experiments) for incomplete data sets, thus reducing the number of potential experiments significantly.

$\small f(\bar w) = w_{000} + w_{011} + w_{101} + w_{110} - w_{001} - w_{010} - w_{100} - w_{111}$

Want to learn more?

We've got you covered!

References

  • Gavryushkin, Alex, and Alexei J. Drummond. "The space of ultrametric phylogenetic trees." Journal of Theoretical Biology 403 (2016): 197-208.

  • Gavryushkin, Alex, Chris Whidden, and Frederick A. Matsen. "The combinatorics of discrete time-trees: theory and open problems." Journal of Mathematical Biology, (2017), doi: http://dx.doi.org/10.1007/s00285-017-1167-9.

  • Beerenwinkel, Niko, Lior Pachter, and Bernd Sturmfels. "Epistasis and shapes of fitness landscapes." Statistica Sinica (2007): 1317-1342.

  • Crona, Kristina, Alex Gavryushkin, Devin Greene, and Niko Beerenwinkel. "Inferring genetic interaction from comparative fitness data." bioRxiv, doi: http://dx.doi.org/10.1101/137372.

  • Lienkaemper, Caitlin, James Drain, Lisa Lamberti, and Alex Gavryushkin. "Inferring genetic interactions from partial fitness orders." bioRxiv, to appear this month.

Acknowledgments

  • Alexei Drummond, University of Auckland
  • Niko Beerenwinkel, ETH Zürich
  • Bernd Sturmfels, Max Planck Institute Leipzig
  • Kristina Crona, American University
  • Devin Greene, American University
  • Lisa Lamberti, ETH Zürich
  • Caitlin Lienkaemper, Max Planck Institute Leipzig

Thanks for your attention!


and stay tuned